Hexawise test coverage graph showing 83.9% coverage in just 20 tests

 

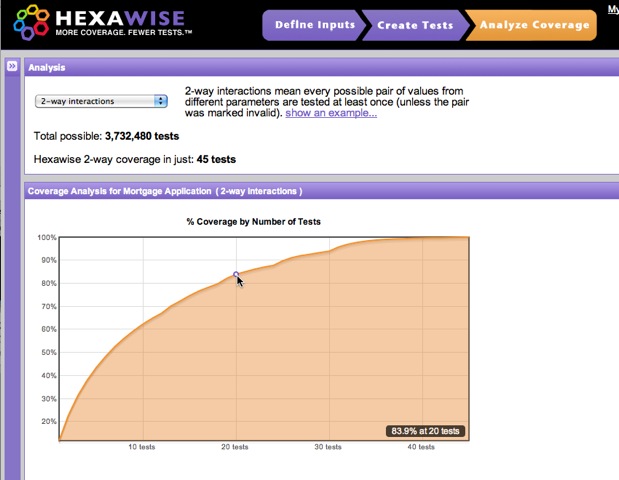
Among the many benefits Hexawise provides is creating a test plan that maximizes test coverage with each new scenario tested. The graph above shows that after just 20 test 83.9% of the test combinations have been tested. Read more about this in our case study of a mortgage application software test plan. Just 48 test combinations are needed to test for every valid pair (3.7 million possible tests combinations exist in this case). If you are lost now, this video may help.

The coverage achieved by the first few tests in the plan will be quite high (and the graph line will point up sharply) then the slope will decrease in the middle of the plan (because each new test will tend to test fewer net new pairs of values for the first time) and then at the end of the plan the line will flatten out quite a lot (because by the end, relatively few pairs of values will be tested together for the first time).

One of the benefits Hexawise provides is making that slope as steep as possible. The steeper the slope the more efficient your test plan is. If you repeat the same tests of pairs and triples and... while not taking advantage of the chance to test, untested pairs and triples you will have to create and run far more test than if you intelligently create a test plan. With many interactions to test it is far too complex to manually derive an intelligent test plan. A combinatorial testing tool, like Hexawise, that maximizes test plan efficiency is needed.

For any set of test inputs, there is a finite number of pairs of values that could be tested together (that can be quite a large number). The coverage chart answers, after each tests, what percentage of the total number of pairs (or triples, etc.) that could be tested together have been tested together so far?

The Hexawise algorithms achieve the following objectives that help testers find as many defects as possible in as few tests as possible. In each and every step of each and every test case, the algorithm chooses a test condition that will maximize the number of pairs that can be covered for the first time in the test case. (Or, the maximum number of triplets or quadruplets, etc. based on the thoroughness setting defined by the user). Allpairs (AKA pairwise) is a well known and easy to understand test design strategy. Hexawise lets users create pairwise sets of tests that will test not only every pair but it also allows test designers to generate far more thorough sets of tests (3-way to 6-way coverage). This allows users to "turn up the coverage dial" and generate tests that cover every single possible triplet of test inputs together at least once (or every 4-way combination or 5-way combination or 6-way combination).

Note that the coverage ratio Hexawise shows is based on the factors entered as items to be tested: not a code coverage percentage. Hexawise sorts the test plan to front load the coverage of the tuple pairs, not the coverage of the code paths. Coverage of code paths ultimately depends on how good a job the test designer did at extracting the relevant parameters and values of the system under test. You would expect there to be some loose correlation between coverage of identified tuple pairs and coverage of code paths in most typical systems.

If you want to learn more about these concepts, I would recommend Scott's Scott Sehlhorst articles on pairwise and combinatorial test design. They are some of the clearest introductory articles about pairwise and combinatorial testing that I have seen. They also contain some interesting data points related to the correlation between 2-way / allpairs / pairwise / n-way coverage (in Hexawise) and the white box metrics of branch coverage, block coverage and code coverage (not measurable by Hexawise).

In Software testing series: Pairwise testing, for example, Scott includes these data points:

 

• We measured the coverage of combinatorial design test sets for 10 Unix commands: basename, cb, comm, crypt, sleep, sort, touch, tty, uniq, and wc... The pairwise tests gave over 90 percent block coverage.

 

• Our initial trial of this was on a subset Nortel’s internal e-mail system where we able cover 97% of branches with less than 100 valid and invalid testcases, as opposed to 27 trillion exhaustive testcases.

 

• A set of 29 pair-wise... tests gave 90% block coverage for the UNIX sort command. We also compared pair-wise testing with random input testing and found that pair-wise testing gave better coverage.

 

Related: Why isn't Software Testing Performed as Efficiently and Effecively as it could be? - Video Highlight Reel of Hexawise – a pairwise testing tool and combinatorial testing tool - Combinatorial Testing, The Quadrant of Massive Efficiency Gains

Specific guidance on how to view the percentage of coverage graph for the test plan in Hexawise:

 

When working on your test plan in Hexawise, to get the checklist to be visible, click on the two downward arrow keys located shown in the image:

Then you'll want to open up the "Advanced" list. So you might need to click here:

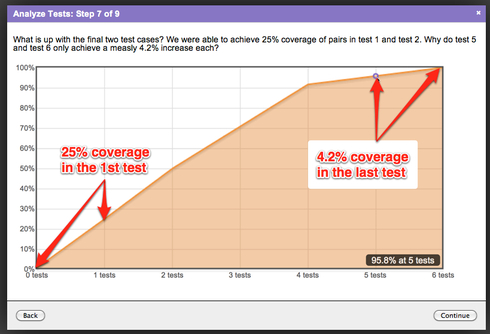
Then the detailed explanation will begin when you click on "Analyze Tests"

 

This post is adapted (and some new content added) from comments posted by Justin Hunter and Sean Johnson.